회귀 알고리즘은 분류에서도 사용된다. 분류의 의미는 정해져 있는 범주들 중 하나로 예측하는 것이다. 이를 카드거래 이상 유무, 스팸메일여부, 고객 이탈 여부, 백혈병 여부 등 분류하는 문제에 활용할 수 있다.
로지스틱 회귀는 샘플이 특정 클래스에 속할 확률을 추정하는데 널리 사용된다. 추정확률이 50%가 넘으면 그 샘플이 해당 클래스에 속한다고 얘기할 수 있다. 클래스에 속한다는 것은, 레이블이 1인 양성클래스(positive class), 클래스에 속하지 않는 것은 레이블이 0인 음성 클래스(negative class0라고 한다. 이를 이진 분류기라 한다.
흔히 로지스틱 회귀는 종속변수가 이항형 문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용된다. 이외에, 두 개 이상의 범주를 가지는 문제가 대상인 경우엔 다항 로지스틱 회귀 (multinomial logistic regression) 또는 분화 로지스틱 회귀 (polytomous logistic regression)라고 하고 복수의 범주이면서 순서가 존재하면 서수 로지스틱 회귀 (ordinal logistic regression) 라고 한다. 즉 로지스틱 회귀는 이항형 또는 다항형이 될 수 있다. 이항형 로지스틱 회귀(binomial logistic regression)의 경우 종속 변수의 결과가 (성공, 실패) 와 같이 2개의 카테고리가 존재하는 것을 의미하며 다항형 로지스틱 회귀는 종속형 변수가 (맑음, 흐림, 비)와 같이 2개 이상의 카테고리로 분류되는 것을 가리킨다. 이항형 로지스틱의 회귀 분석에서 2개의 카테고리는 0과 1로 나타내어지고 각각의 카테고리로 분류될 확률의 합은 1이 된다.
<작동 원리>
선형회귀와 비슷하게 가중치 합을 계산하고 편향을 더한다. 그러나 종속 변수와 독립 변수 사이의 관계에 있어서 선형 모델과 차이점을 지니고 있다. 첫 번째 차이점은 이항형인 데이터에 적용하였을 때 종속 변수 y의 결과가 범위[0,1]로 제한된다는 것이고 두 번째 차이점은 종속 변수가 이진적이기 때문에 조건부 확률(P(y│x))의 분포가 정규분포 대신 이항 분포를 따른다는 점이다.
로지스틱 함수는 은 0과 1사이를 출력하는 시그모이드 함수이다. 즉, 로지스틱 함수는 시그모이드 함수라고도 한다.
로지스틱 함수는 𝑥값으로 어떤 값이든 받을 수가 있지만 출력 결과는 항상 0에서 1사이 값이 된다. 즉, 확률밀도함수(probability density function) 요건을 충족시키는 함수인 것이다. S자 형태의 단순 증가 혹은 단순 감소 그래프이다.
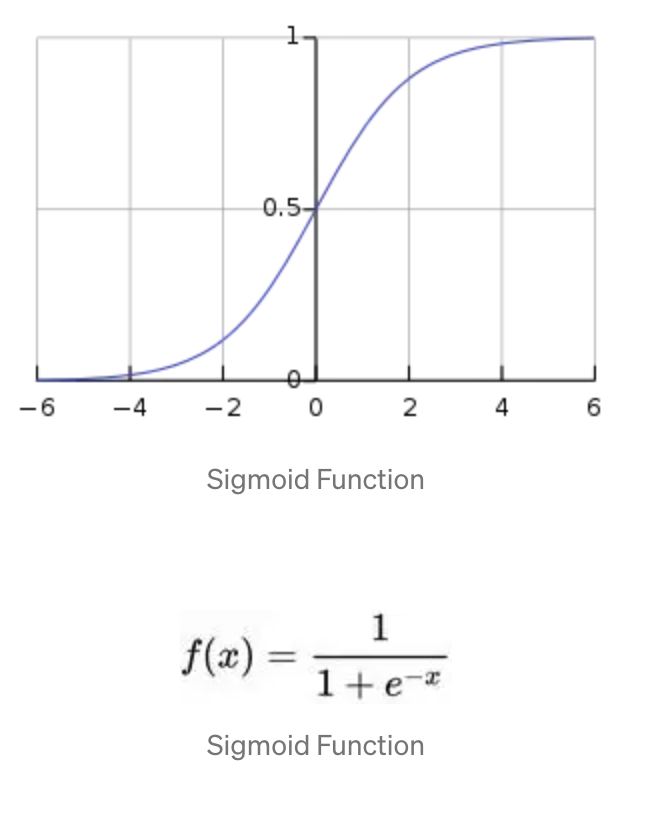
위 식에서 x는 선형 회귀 형태로 다음과 같다

odds(승산)은 이러한 x의 해석을 용이하게 한다는 개념에서 등장한다. 승산은 임의의 사건 𝐴가 발생하지 않을 확률 대비 일어날 확률의 비율로, p가 성공확률이라면 실패 대비 성공확률의 비율이다. 다음 식 처럼 표현할 수 있다.

p에 로지스틱 함수를 넣으면 odd는 결국 범주 0(음성클래스)에 속할 확률 대비 범주 1(양성클래스)에 속할 확률이 된다.
odds에 log를 취하면

단순한 선형결합 형태로 변하게 된다 . 이를 로짓 변환이라고 한다.

사이킷런에서 구현해봅시다
유명한 iris 데이터에서 꽃잎의 너비로 Iris-Versicolor을 감지하는 이진 분류기를 만들어볼 것입니다.
사이킷런의 logisticRegression은 클래스 레이블을 반환하는 predict()와 클래스에 속할 확률을 반환하는 predict_proba()가 있습니다.
from sklearn import datasets
iris=datasets.load_iris()
#꽃잎의 너비로 Iris-Versicolor을 감지하는 이진 분류기를 만들어보자
import numpy as np
X=iris['data'][:,3:]#꽃잎의 너비만
y=(iris['target']==2).astype(np.int32) #Iris-Versicolor면 1, 아니면 0
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X,y)
import matplotlib.pyplot as plt
newX=np.linspace(0,3,1000).reshape(-1,1)
yProba = lr.predict_proba(newX)
plt.plot(newX,yProba[:,1],"g",label="Iris-Versicolor")
plt.plot(newX,yProba[:,0],"b--",label="NOT Iris-Versicolor")
초록색 라인을 보면 우리가 찾는 Iris-Versicolor 품종의 꽃잎 너비는 1,4~2.5cm에 분포합니다. 반면 다른 품종은 일반적으로 꽃잎의 너비가 더 작아 0.1~1.8cm에 분포합니다. 꽃잎의 너비가 2cm이상이면 Iris-Versicolor 클래스에 대한 높은 확률을 출력합니다. 이 두 극단에서는 겹치는 부분이 있어 분류가 확실하지 않지만, 어쨌든 분류하려고 하면(predict_proba()가 아닌 predict()를 사룔해서) 가장 가능성이 큰 클래스를 반환할 것입니다. 그렇기에 양쪽 확률이 똑같이 50%가 되는 1.6cm근방에서 결정 경계가 만들어질 것입니다.

code:
https://colab.research.google.com/drive/15vQxtl97V3lCS1fyOIzT7pTILaEbKD41?usp=sharing
'머신러닝' 카테고리의 다른 글
| 차원 축소, PCA python 사이킷런 (0) | 2022.12.05 |
|---|---|
| 다중 로지스틱 회귀 (소프트맥스 회귀) (0) | 2022.12.05 |
| [머신러닝4] Logistic Regression 로지스틱 회귀 pyhton (0) | 2022.11.30 |
| [머신러닝3] Multiple Linear Regression 다중선형회귀 python (0) | 2022.11.30 |
| [머신러닝2] Polynomial Regression python (0) | 2022.11.30 |